Most of the services provided by the Beidou system are very easy to understand. Some friends may ask, what is the timing?
In simple terms, time service refers to the transmission of standard time.
In fact, the need for timing has existed since ancient times. We can see buildings like bell towers in many cities in China.
The clock tower is a tool for transmitting time to a city. Everyone knows what time it is when they hear the bell, so they can go and do the corresponding things.
We know that the current international standard time is called Coordinated Universal Time (UTC), which is based on the second length of atomic time and combined with the time of Universal Time. When the difference between the two accumulates year by year, reaching 0.9 seconds, the error is compensated by a plus or minus 1 leap second approach while maintaining a uniform time scale.
The time service of the Beidou system is to transmit the Chinese standard time of the National Time Service Center of the Chinese Academy of Sciences to applications in all walks of life through satellite services to ensure the synchronization and accuracy of time.
How to use satellite positioning
The satellite will regularly send signals to the outside, and our signal receiver locates by receiving the satellite's signal.
Assuming there are two satellites now, each maintaining its own clock. Assuming that each satellite sends a signal every second. At the same time, the receiver also maintains its own clock, so the receiver can calculate the distance between itself and two satellites by judging the arrival time of the signal.
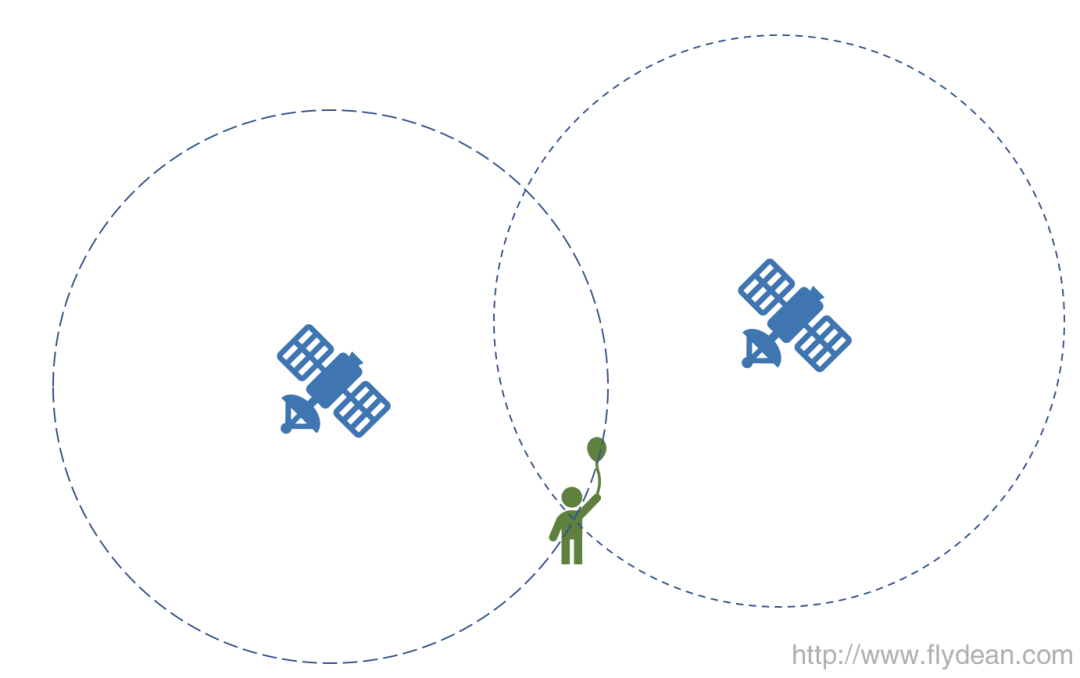
Note that above we assume that the receiver has its own accurate clock. We will provide a detailed explanation for the discussion of this issue later.
What we drew above is a two-dimensional schematic diagram. If in a three-dimensional environment, the corresponding number of satellites needs to be added by one.
Okay, the question is, can we accurately locate our position by knowing the distance between the two satellites?
The answer is no, because we do not know the location of the satellite.
01
Ephemeris and satellite positions
How can we accurately locate the position of the satellite?
As early as 1617, Johannes Kepler, the great god, used seven elements in an idealized model to locate a satellite orbit.
Of course, this idealized model has some constraints: the orbit adheres to a 2D plane and is always elliptical. Then, you can use the following elements to accurately describe this fixed orbit:
The average of the major and minor axes of an ellipse (in fact, the area of the ellipse, A)
The ratio of the major axis to the minor axis of an ellipse (e).
Three parameters describing the direction of the Orbital plane: inclination (i0),
The longitude of the ascending node (Ω 0),
Periapsis( ω)
What is the distance of the satellite along the ellipse at T=0 (average near point angle M0)
Time at T=0 (t0e)
Although Kepler's model is perfect enough, it is not enough, because the earth itself is not a perfect sphere, and the Gravitational field is not completely uniform. If this model is directly used, there may be a kilometer error in satellite position.
In order to solve this problem, the great god of GPS was designed in 1970, and six parameters were added to the Kepler model.
The following figure shows the positioning parameters used by GPS and European Galilean moons satellite system:
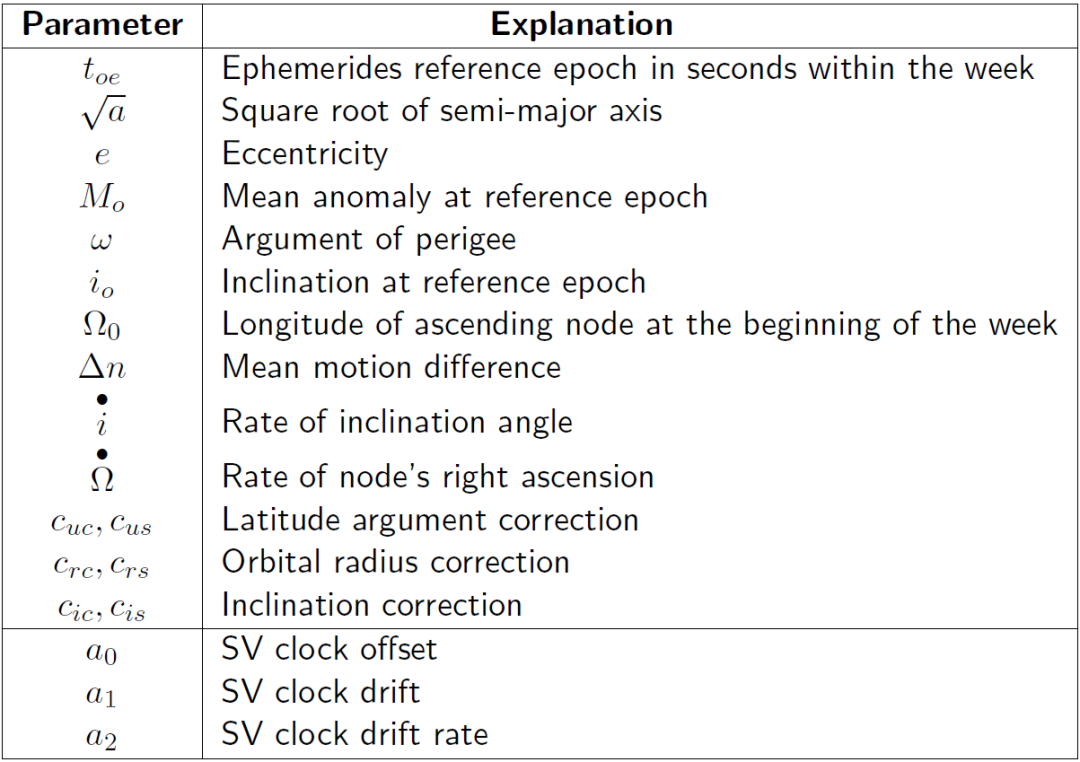
I won't go into detail about the specific meaning. Interested friends can explore it on their own.
The Beidou satellite system also uses GPS designed satellite positioning parameters.
By number C06@0 Taking the Beidou satellite as an example, let's take a look at the signal information it provides externally:
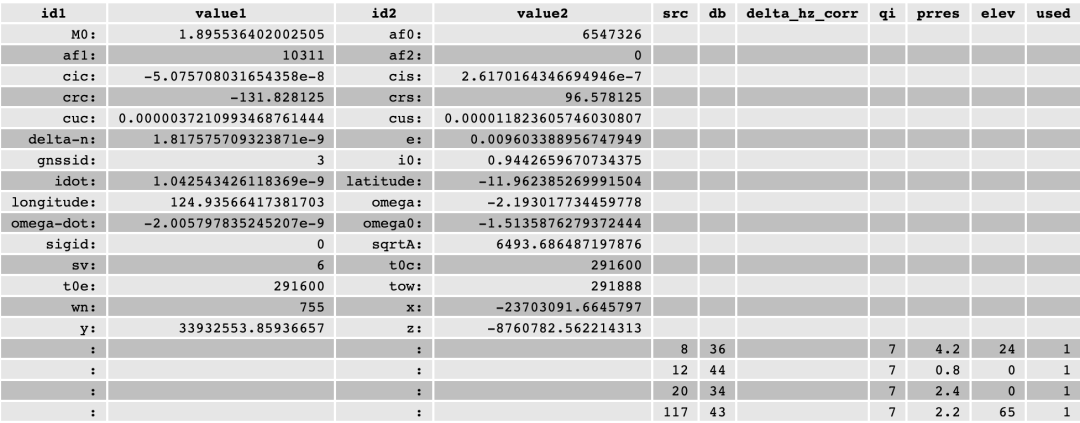
如果我们把当前的卫星位置和之后可预测的卫星位置统计起来,就生成了一张星历表。

The above figure shows the Ephemeris of Beidou satellite on June 24, 2020.
02
Unknown clock
With the position and distance from the satellite, we can calculate our position. But there is a premise here that the satellite's clock is accurate, and the receiver's clock is also accurate.
There are two issues involved here, one is the accuracy of the satellite's clock, and the other is the accuracy of the receiver's clock.
Let's first take a look at the issue of receiver clock accuracy.
If the signal propagates at the speed of light, the error distance of one nanosecond is 30 centimeters.
For ordinary receiving devices, maintaining an accurate clock at the nanosecond level is basically impossible, so how can ordinary receiving devices also be able to accurately locate?
The answer is to add another satellite.

The receiving device receives three signals at the same time, and the signals at the same time must converge at the receiver's actual position. Therefore, the receiver can correct the local clock to gather multiple satellite signals at one point, thereby achieving local clock correction and precise positioning. Kill two birds with one stone.
If it is in three-dimensional space, at least 4 satellites are required.
03
Accurate clock
We have solved the problem with the receiver, how can we solve the problem with the sender?
Each satellite also needs an accurate clock to send signals.
We know that the most accurate time in the world is generated in a laboratory environment, but the environment in which satellites are located cannot achieve the precision of a laboratory.
We can monitor the clock in the air from the ground and compare it with the precise time in the laboratory environment, and then send verification information to the satellite.
There are three main correction items:
Clock offset af0 nanoseconds
Clock skew rate af1 nanoseconds/second
Clock skew acceleration af2 ns/s/s
Generally speaking, satellites do not adjust their own clock after receiving correction information, but instead send the correction item and the original clock to the receiving party for processing.
Ionospheric error correction
Okay, all the problems seem to have been solved, but there is still one more problem. It's about the ionosphere.
The transmission of signals in the ionosphere will be affected, resulting in delays.
How to solve the problem of signal delay?
Because the delay generated by the ionosphere is proportional to the signal frequency. Therefore, we can use multi frequency signals to derive the total delay generated and eliminate the total delay based on the time difference of arrival between different frequency bands.
This can eliminate over 99.9% of errors introduced by the atmosphere without the need for further modeling.
When we introduced the Beidou system above, we mentioned that the Beidou system uses signals in three frequency bands B1, B2, and B3, and using these signals can better eliminate ionospheric errors.
It is said that GPS has two frequency bands.
上一篇:China Space Day Xichang Satellite Launch Center prepares for 下一篇:Shenzhou XIV was successfully launched, and China entered th




